Leecode #576. 出界的路径数

给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。

示例

示例 1：

输入: m = 2, n = 2, N = 2, i = 0, j = 0 输出: 6 解释:

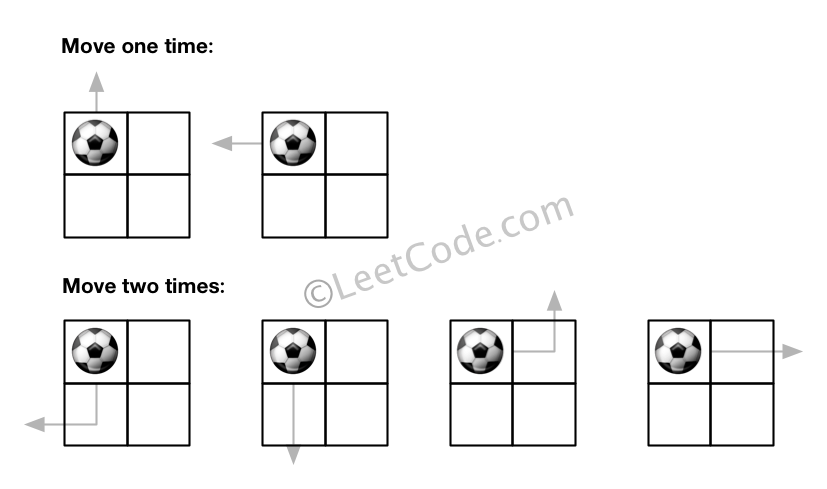
示例 2：

输入: m = 1, n = 3, N = 3, i = 0, j = 1 输出: 12 解释:

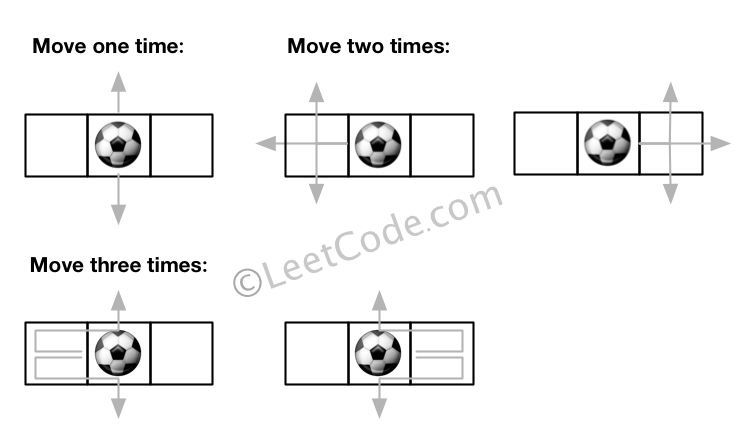
解题思路

​ 遇到这种题目，很容易就想到dfs，然而超时了，因为走过的格子可以再走，这样就增加了很多可能性，可以将dp的思想结合在一起，用数组arr[n][x][y]保存在坐标x，y还剩n次移动的时候能有多少种可能性，这种保存状态的方式可以极大的提高运行速率。

​ 今天又学到一个新的技能，python自带的装饰器lru_cache，可以缓存函数输入与输出，如果第二次调用函数且输入参数相同，可以直接从缓存中返回函数值，赞~

class Solution:
    def findPaths(self, m: int, n: int, N: int, i: int, j: int) -> int:
        from functools import lru_cache
        @lru_cache(None)
        def dfs(x, y, count):
            if count > N:
                return 0 
            if x<0 or x >=m or y <0 or y >= n:
                return 1
            rlt = 0
            for dx, dy in ((0, 1), (0, -1), (1, 0), (-1, 0)):
                rlt += dfs(x-dx, y-dy, count+1)
            return rlt
                
        return dfs(i, j, 0) % (10 ** 9 + 7)