Leecode #332. 重新安排行程[Hierholzer 算法]
给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。
说明:
如果存在多种有效的行程,你可以按字符自然排序返回最小的行程组合。例如,行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小,排序更靠前 所有的机场都用三个大写字母表示(机场代码)。 假定所有机票至少存在一种合理的行程。
示例
示例 1:
输入: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
输出: ["JFK", "MUC", "LHR", "SFO", "SJC"]
示例 2:
输入: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出: ["JFK","ATL","JFK","SFO","ATL","SFO"]
解释: 另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。
解题思路
1. DFS + 回溯
一开始觉得这就是简单的深度优先搜索问题,遍历节点然后删除节点之间的边,若没有遍历完全部的节点,则将边恢复
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
l = len(tickets)
airline = defaultdict(list)
for begin, end in tickets:
# 通过bisect进行二分插入
bisect.insort(airline[begin], end)
ret = []
def dfs(begin, count):
ret.append(begin)
# 判断是否遍历完全部的节点
if count == l:
return True
for i in range(len(airline[begin])):
t = airline[begin][i]
# 删除 begin -> t的这条边
airline[begin].pop(i)
# 遍历节点t,若成功,直接返回
if dfs(t, count+1):
return True
# 若不成功,回溯
airline[begin].insert(i, t)
# 说明从这个节点开始的线路没有一个ok的,所以弹出
ret.pop()
dfs('JFK', 0)
return ret
2. Hierholzer 算法
要一次按顺序走完全部的机票,其实可以转换成一笔画问题。
这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系,下面给出定义:
通过图中所有边恰好一次且行遍所有顶点的通路称为欧拉通路。
通过图中所有边恰好一次且行遍所有顶点的回路称为欧拉回路。
具有欧拉回路的无向图称为欧拉图。
具有欧拉通路但不具有欧拉回路的无向图称为半欧拉图。
因为本题保证至少存在一种合理的路径,也就告诉了我们,这张图是一个欧拉图或者半欧拉图。我们只需要输出这条欧拉通路的路径即可。
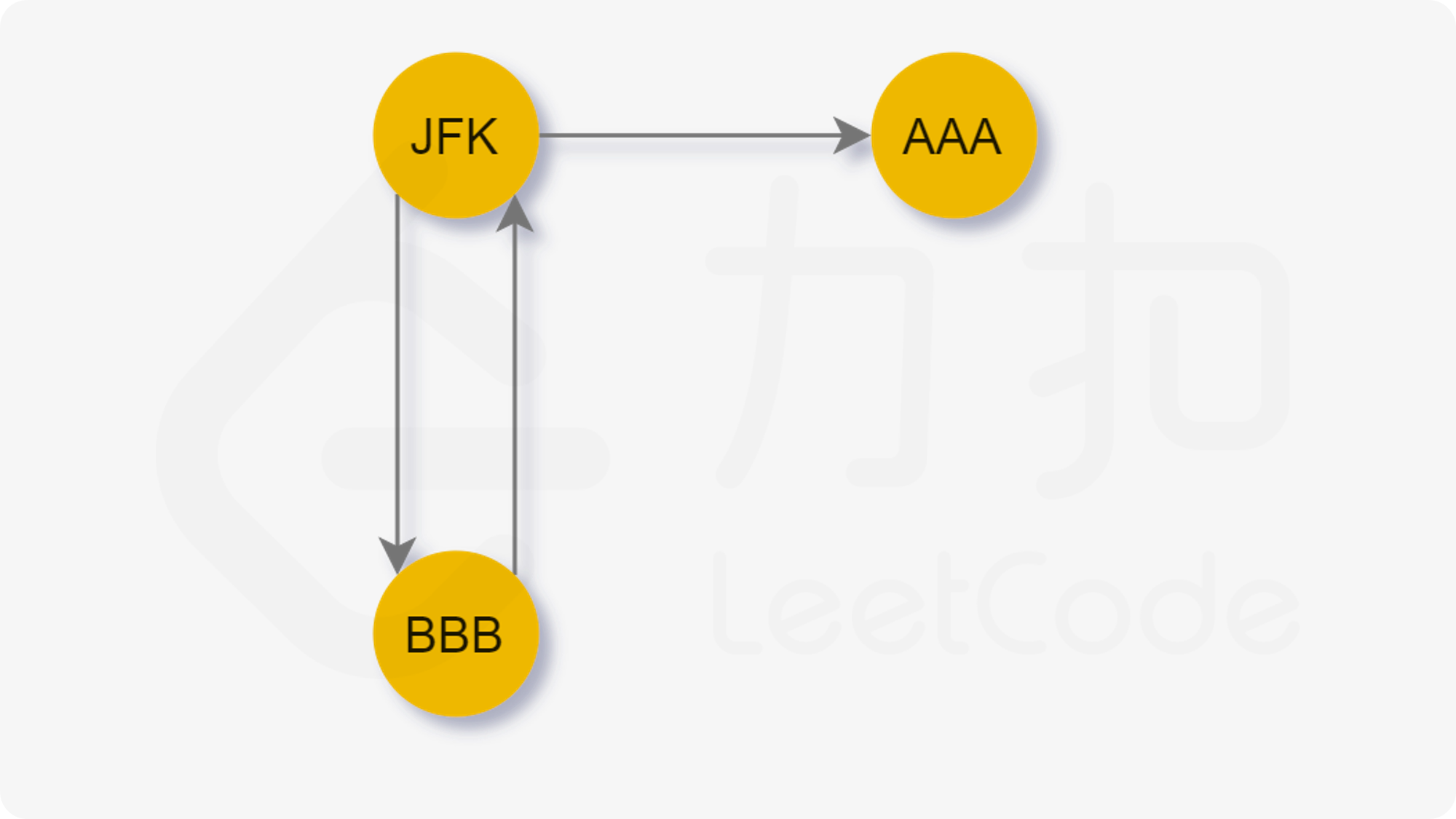
考虑从节点JFK出发,根据贪心算法先选择AAA,那么就进入了死胡同,导致无法遍历其他节点就停止了;方法1是遇到这种情况的时候将AAA重新加入航线,然后遍历BBB,回过头来再遍历AAA,完成线路。但是这样的方法重复访问了AAA,Hierholzer算法中只用将遇到死胡同的线路压栈,这样就避免了重复访问。
-
从起点出发,进行深度优先搜索。
-
每次沿着某条边从某个顶点移动到另外一个顶点的时候,都需要删除这条边。
-
如果没有可移动的路径,则将所在节点加入到栈中,并返回。
整个图中,肯定只能存在一个[死胡同],这个死胡同节点肯定是最后被访问的,而且遍历他相连的其他节点最后肯定能返回,因此dfs遍历到这个死胡同开始返回,因此死胡同是第一个压栈的元素
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
airline = defaultdict(list)
for begin, end in tickets:
bisect.insort(airline[begin], end)
ret = []
def dfs(begin):
while airline[begin]:
dfs(airline[begin].pop(0))
ret.insert(0, begin)
dfs('JFK')
return ret
